We have to find the probability of selecting a white ball on the second draw given that the first ball drawn was green.
We know that probability of selecting a green ball and then a white ball without replacement is 0.15, so we can write:
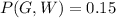
We also know that the probability of selecting a green ball in the first draw is 0.65:
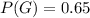
Then, we can use this to find the conditional probability of selecting a white ball on the second draw given that the first ball drawn was green can be calculated as:
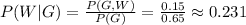
Answer: the probability is 0.231.