Question

You have a 6-m-long copper wire. You want to make an N-turn current loop that generates a 4.085 mT magnetic field at the center when the current is 1.513 A. You must use the entire wire. What will be the diameter, in cm, of your coil?

Answer 1

2.98 cm

Explanation:

Given:

Length wire (L) = 6 m

Current (i) = 1.513 A

magnetic field (β) = 4.085 mT = 4.085 x 10^-3 T

Magnetic field at the center of circular coil is given for the following formula:

`\beta=(\mu_0\cdot N\cdot i)/(2R)=(\mu_0\cdot N\cdot\imaginaryI)/(d)`

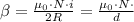
The total length of wire in the coil is given by:

`\begin{gathered} L=\pi\cdot d\cdot N \\ \\ N=(L)/(\pi d) \end{gathered}`

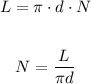
We replacing:

`\begin{gathered} \beta=(\mu_0\cdot(L)/(\pi d)\cdot\imaginaryI)/(d) \\ \\ \beta=(\mu_0\cdot L\cdot\imaginaryI)/(\pi\cdot d^2) \\ \\ d^2=(\mu_0\cdot L\cdot\imaginaryI)/(\pi\beta) \\ \\ d=\sqrt{(\mu_0L\imaginaryI)/(\pi\beta)} \\ \\ \text{ Therefore:} \\ \\ d=\sqrt{(4\pi\cdot10^(-7)\cdot6\cdot1.513)/(\pi\cdot4.085\cdot10^(-3))} \\ \\ d=0.0298\text{ m}=2.98\text{ cm} \end{gathered}`

Therefore, the diameter in centimeters is equal to 2.98 cm