SOLUTION
Write out the equation for the relation
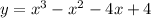
The X-intercept is the value of x when y is equated to zero
hence if Y=o, the equation will be
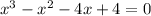
Then, using factor method
Substitute x=1 into the equation
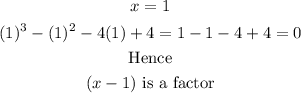
Similarly,

Similarly,
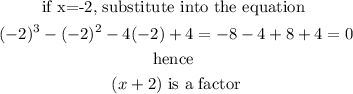
Therefore, the factored form of the equation is
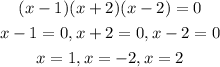
Then the x-intercepof the relation given is
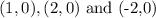
The Y-intercept is the value of Y when x is zero
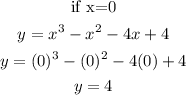
Hence, the Y-intercept is (0,4)
Therefore
x-intercept is (-2,0), (1,0), (2,0), and Y-intercept is (0,4)
The Last option is Correct (D)