Question

How to find the inverse of each function. Then graph the function and its inverse. f(x)= 3x + 12

Answer 1

Given the function:

`f(x)=3x+12`

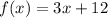
To find the inverse,

step 1: Let y represent f(x).

Thus,

`\begin{gathered} f(x_)=3x+12 \\ where\text{ y=f\lparen x\rparen} \\ \Rightarrow y=3x+12 \end{gathered}`

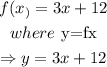
step 2: Swap the position of y for x.

Thus,

`x=3y+12`

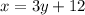
step 3: Make y the subject of the equation in step 2.

Thus,

`\begin{gathered} x=3y+12 \\ subtract\text{ 12 from both sides of the equation,} \\ x-12=3y+12-12 \\ \Rightarrow x-12=3y \\ divide\text{ both sides by the coefficient of y, which is 3} \\ (x-12)/(3)=(3y)/(3) \\ (x)/(3)-(12)/(3)=y \\ \Rightarrow y=(1)/(3)x-4 \end{gathered}`

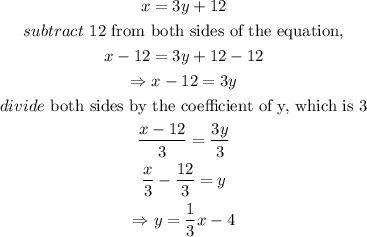
Thus, the inverse of the function is

`f^(-1)(x)=(1)/(3)x-4`

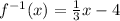
The graphs of the function and its inverse are as shown below: