Question

For a mass - spring system that undergoes a simple harmonic motion with amplitude A , determine the position x at which the kinetic energy is equal to 3 times the potential energy ( KE = 3 PE ) .

Answer 1

The elastic potential energy of a spring is given by:

`PE=(1)/(2)kx^2`

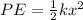
Where:

`\begin{gathered} PE=\text{ potential energy} \\ k=\text{ spring constant} \\ x=\text{ distance of the spring is compressed} \end{gathered}`

Now, the total energy of the spring is given when the value of "x" is equal to the amplitude "A":

`E_(tot)=(1)/(2)kA^2`

The total energy is converted into kinetic energy and elastic energy, therefore, we have:

`(1)/(2)kA^2=(1)/(2)kx^2+(1)/(2)mv^2`

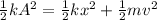
Since the kinetic energy is twice the potential energy we have:

`(1)/(2)mv^2=2((1)/(2)kx^2)=kx^2`

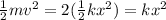
Now, we substitute the values in the equation:

`(1)/(2)kA^2=(1)/(2)kx^2+kx^2`

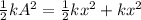
Now, we can cancel out the spring constant "k":

`(1)/(2)A^2=(1)/(2)x^2+x^2`

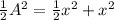
Now, we add like terms in the right side:

`(1)/(2)A^2=(3)/(2)x^2`

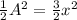
Now, we multiply both sides by 2:

`A^2=3x^2`

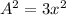
Now, we divide both sides by 3:

`(A^2)/(3)=x^2`

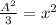
Now, we take the square root to both sides:

`\sqrt{(A^2)/(3)}=x`

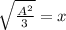
Solving the operations:

`\pm0.5A=x`

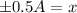
Therefore, the distance is 0.5A.