ANSWERS
• m∠B = 59°
,
• m∠C = 81°
,
• c = 230.5 cm
Step-by-step explanation
Let's draw a diagram of this triangle first,
Given:
• a = 150 cm
,
• b = 200 cm
,
• m∠A = 40°
Find c, C and B.
First, with the given information, we can apply the law of sines to find B,
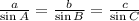
For this problem, we have to use the first two fractions,
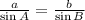
Replace with the known values,
![\frac{150\operatorname{cm}}{\sin40}=\frac{200\operatorname{cm}}{\sin B}]()
To solve for B, first raise both sides of the equation to -1 - in other words, flip the fractions,
![\frac{\sin40}{150\operatorname{cm}}=\frac{\sin B}{200\operatorname{cm}}]()
Multiply both sides by 200cm,
![\begin{gathered} \frac{\sin40}{150\operatorname{cm}}\cdot200cm=\frac{\sin B}{200\operatorname{cm}}\cdot200\operatorname{cm} \\ \frac{200\operatorname{cm}}{150\operatorname{cm}}\sin 40=\sin B \end{gathered}]()
And use the inverse of the sine to find B,
![B=\sin ^(-1)(\frac{200\operatorname{cm}}{150\operatorname{cm}}\sin 40)]()
The three equations you can't see above are in the following picture,
Solve with a calculator: B = 59°
To find the third angle C, we know that the interior angles of any triangle add up to 180°. Thus, for this triangle,
• A + B + C = 180°
Solve for C,
• C = 180° - A - B
Replace with the values
• C = 180° - 40° - 59°
• C = 81 °
Then, using the law of sines again, we can find the length of side c.
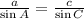
Solve for c and replace with the values,
![c=a\cdot(\sin C)/(\sin A)=150\operatorname{cm}\cdot(\sin81)/(\sin40)=230.5\operatorname{cm}]()
The two equations you can't see above are in the following picture,
The length of side c is 230.5 cm