Question

I need help please. I don’t know how to do this

Answer 1

Given- The set of inequalities,

`3x+43x-10}`
`-4x-3\leq2x+9\text{ and -3x+2>-2x+5}`
`4(x+1)\ge3(x+2)\text{ and -3\lparen x-1\rparen<5\lparen x+2\rparen}`
`4x-6\leq5x+6\text{ and -3x-2>2x+8}`

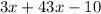
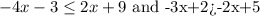
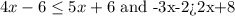
Required- To find out which one of these inequalities have no solution.

Explanation- The inequality which does not give any possible value of the variable will result in no solution.

Now, consider the first inequality,

Solving the inequality further,

`3x+4\lt x-8\text{ and -5x+4\gt3x-10}`
`3x-x<-8-4\text{ and -5x-3x>-10-4}`
`2x<-12\text{ and -8x>-14}`
`which\text{ gives us , }x<-6\text{ and }x<(14)/(8)`

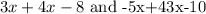
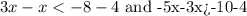
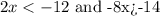
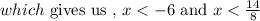
which will give us many solutions such as -7,-8,-9,

and so on.

The values of x that are less than 14/8 and -6 exists.

Remember to change the sign of inequality while multiplying it by negative number.

Now similarly if we solve our second inequality for x we get,

`x\ge-2\text{ and }x<-3`

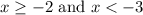
This is the inequality that will result in no solution. Since,

`\begin{gathered} x\ge-2\text{ gives , }x=\text{ -2,-1,0,1 etc and} \\ x<-3\text{ gives, }x=-4,-5,-6\text{ and so on } \end{gathered}`

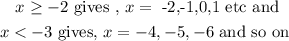
As there is no possible value of x that satisfies both our inequality. Hence equality 2 will result in no solution.

Final Answer- Option B