Given:
John takes 8 hours to do 4 people's hair.
a.) The unit rate.
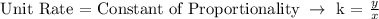
Let,
x = No. of hours ; The no. of hours the hairstylist took/invested.
y = No. of people ; This is the output of the hairstylist.
We get,
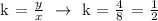
Therefore, the equation in getting the no. of haircuts will be,
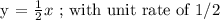
b.) How many haircuts could John do in 2 hours. Let, x = 2.
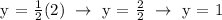
Therefore, John could do 1 haircut in 2 hours.
c.) How many haircuts will there be in 5 hours? Let, x = 5.
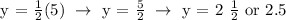
Therefore, there will be 2 1/2 haircuts in 5 hours.