Solution:
Let the points awarded to outer ring region be represented with x
Let the points awarded to bull's eye region be represented with y
Given that
Tom went first and landed 5 arrows in the outer ring and 4 arrows in the bull's-eye, for a total of 363 points. This can be represented by
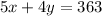
Gabrielle went second and got 1 arrow in the bull's-eye, earning a total of 57 points.
This can be represented as
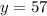
Solving the equation, we have
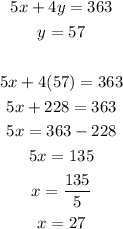
Thus,
The outer ring is worth 27 points, and the bull’s eye is worth 57 points.