B
1) Let's redo the steps Heather did when calculating this. Note that direct variation can be generally written as:
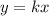
2) Heather was told that when y=8 then z=8 so let's find the constant of proportionality (k) plugging into the formula below into y and z the given values:

Now we know the value of k, let's test that and then mark the right choice
![\begin{gathered} y^3=k\cdot z \\ y³=64\cdot8 \\ y=\sqrt[3]{512} \\ y=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o22ncr28rec3wb1rp10ohk37e5yjracqpg.png)
The first error then was:
b. She substituted incorrectly when calculating the constant of variation.