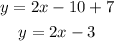Given the point (5, 7) and the slope 2, using the point-slope form we have the equation of the line:
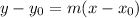
Where m is the slope and x₀ and y₀ are the coordinates of the given point. From this problem, we identify m = 2, x₀ = 5, and y₀ = 7. Then:
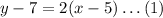
The slope-intercept form is given by:
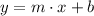
Where m is the slope and b is the y-intercept. Using equation (1):