SOLUTION:
Step 1:
In this question, we are given the following:
A pipefitter must connect a pipeline to a tank as shown in the figure.
The run from the pipeline to the tank is 64ft 6in., while the set (rise) is 35ft 9in.
Step 2:
A. How long is the connection?
Converting 64 feet 6 inches to inches, we have that:
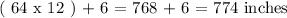
Also, we have 35 feet 9 inches, we have that:
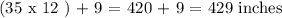
Using Pythagoras' Theorem, we have that:

The length of the connection = 73 feet 9 inches
Step 3:
Will the pipe fitter be able to use standard pipe fittings?
From the diagram, we can see that:
