Given:
The admission fee at an amusement park is $4.25 for children and $7.20 for adults.
Let the number of children = x
Let the number of adults = y
On a certain day, 333 people entered the park
so, we have the following equation:
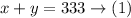
And, the admission fees collected totaled $1843
so, the equation will be:

We will solve the equations (1) and (2)
From equation (1):

substitute with (x) from equation (3) into equation (2):

solve the equation to find y:
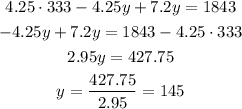
Substitute with (y) into equation (3) to find the value of (x):
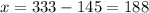
So, the answer will be:
The number of children = x = 188
The number of adults = y = 145