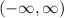Question

ctions,f(x) = x2 - 6x + 9 and g(x) = x - 3Step 2 of 2: Find the domain of(*)(*)(X). Express your answer in interval notation.AnswerDomain in interval notation:

Answer 1

The domain of a function is the set of all values that go into a function. Our function is

`((f)/(g))(x)=(f(x))/(g(x))=(x^(2)-6x+9)/(x-3)`

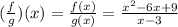
To find the domain, first let's rewrite the numerator as a product of binomials

`x^2-6x+9=(x-3)^2`

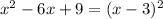
Then, our function is

`((f)/(g))(x)=(x^(2)-6x+9)/(x-3)=((x-3)^2)/(x-3)=x-3`

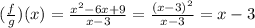
Our function is a line equation, and a line is defined everywhere, therefore, the domain of our function is

`(-\infty,\infty)`