Explanation.
To find the area of the figure, we will have to split the figure into different parts as following
We have 5 different parts
So the scope will be to find each of the areas and then sum them up
For part A
The area of a will be
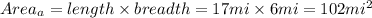
For part B
Area of B will be found to be
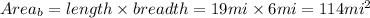
Part C
The figure is a quadrant
The area of a quadrant is
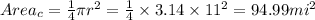
For part D
The figure is a rectangle
The area of the rectangle
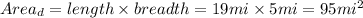
Finally for part E
We will find the area of the triangle
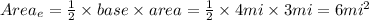
The area of the figure is the sum of all values of A, B, C, D, and E
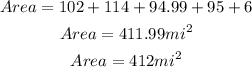
The area of the figure is approximately 412 square miles