Question

A basketball team sells tickets that cost $10, $20, or for VIP seats. $30. The team has sold 3138 tickets overall. It has sold 160 more $20 tickets than $10 tickets. The total sales are $59, 060. How many tickets of each kind have been sold?How many $10 tickets were sold?

Answer 1

• The number of $10 tickets sold = 1116

,

• The number of $20 tickets sold = 1276

,

• The number of $30 tickets sold = 746

Step-by-step explanation:

• Let the number of $10 tickets sold = a

,

• Let the number of $20 tickets sold = b

,

• Let the number of $30 tickets sold = c

The team has sold 160 more $20 tickets than $10 tickets.

`b=a+160\cdots(1)`

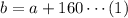
The team has sold 3138 tickets overall, thus: a+b+c = 3138...(2)

Substitute b=a+160 from (1) into equation (2).

`\begin{gathered} a+\mleft(a+160\mright)+c=3138 \\ 2a+c=3138-160 \\ 2a+c=2978\cdots(3) \end{gathered}`

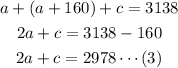
If the total sales are $59,060, then: 10a+20b+30c=59,060...(4)

Substitute b=a+160 from (1) into equation (4).

`\begin{gathered} 10a+20\mleft(a+160\mright)+30c=59,060 \\ 10a+20a+3200+30c=59,060 \\ 30a+30c=59,060-3200 \\ 30a+30c=55,860 \\ \text{Divide all through by 30} \\ (30a)/(30)+(30c)/(30)=(55,860)/(30) \\ a+c=1862\cdots(5) \end{gathered}`

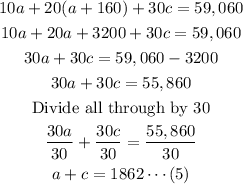
Next, solve equation (3) and (5) simultaneously for a and c:

`\begin{gathered} 2a+c=2978\cdots(3) \\ a+c=1862\cdots(5) \\ \text{Subtract:} \\ a=1116 \\ \text{From (5): }a+c=1862 \\ 1116+c=1862\implies c=1862-1116\implies c=746 \end{gathered}`

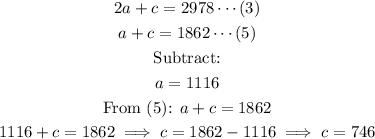
Finally, from equation (1):

`b=a+160=1116+160=1276`

The values of a, b and c are 1116, 1276 and 746 respectively.

Therefore:

• The number of $10 tickets sold, a = 1116

,

• The number of $20 tickets sold, b = 1276

,

• The number of $30 tickets sold, c = 746