Question

An object is placed 15.0 cm in front of a concave lens with a focal length of 8.00 cm. Find the image distance.

Answer 1

Given:

The object distance is,

`u=15.0\text{ cm}`

The focal length is,

`f=8.00\text{ cm}`

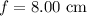
To find:

The image distance

Step-by-step explanation:

The lens formula gives,

`(1)/(v)-(1)/(u)=(1)/(f)`

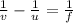
For the concave lens, the focal length is negative and the object distance is negative as per the sign convention. So we write,

`\begin{gathered} (1)/(v)-(1)/(-15.0)=(1)/(-8.00) \\ (1)/(v)=-(1)/(8.00)-(1)/(15.0) \\ (1)/(v)=-(23)/(120) \\ v=-(120)/(23) \\ v=-5.22\text{ cm} \\ The\text{ }negative\text{ sign indicates the image is virtual and in front of the lens} \end{gathered}`

Hence, the image is 5.22 cm in front of the lens.