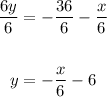Given the following equation provided in the exercise:
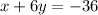
You can solve for the variable "y" by following the steps shown below:
1. You must apply a property called "Subtraction property of equality". This states that:
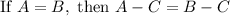
So you must subtract "x" from both sides of the equation:
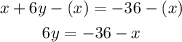
2. Finally, you must apply the "Division property of equality". This states that:
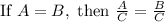
Then, dividing both sides of the equation by 6, you get the equation solved for "y" is: