a) We have to find the amount that have to be deposited each quarter at 8% compounded quarterly to reach $16,000 in 17 years.
We can use the formula for the future value of an annuity as:
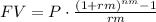
where the annual nominal rate is r = 0.08, the number of periods is n = 17, the number of subperiods per year is m = 4 and the future value is FV = 16000.
Replacing with the known values we can calculate P, the deposit, as:
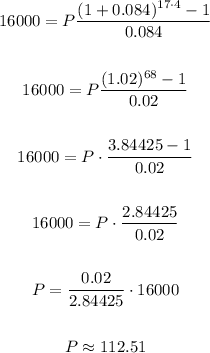
b) If the nominal interest is 6% instead of 8% we can calculate the deposit needed as:

Answer:
a) $ 112.51
b) $ 136.97