Question

Find the sum of the first six terms of the geometric series 2 - 10 + 50 +..

Answer 1

4th option: -5208

Explanation:

A geometric sequence is formed by multiplying a term by a number called the common ratio r to get the next term. The formula for a sum of a geometric sequence is:

`S_n=(a_1\left(1-r^n\right))/(1-r)`

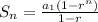
Where a1 is the first term, r is the commom ratio, and n is the number of the term.

The value of r is found as follows:

`r=(-10)/(2)=(50)/(-10)=-5`

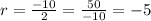
We substitute in the main formula, like this:

`\begin{gathered} S_n=(2\cdot\left(1-\left(-5\right)^6\right?)/(1-\left(-5\right))=(2\cdot\left(1-15625\right))/(1+5)=(2\cdot\left(-15624\right))/(6) \\ S_n=-5208 \end{gathered}`

The sum of the geometric series is equal to -5208