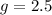Question

What value of g makes the equation 2g + 6 - 14g = -6(9 - 5) true? 6 © Record the answer and fill in the bubbles on the grid provided. Be sure to use the correct place value. Copyright ©

Answer 1

Given the following equation:

`2g+6-14g=-6\mleft(9-5\mright)`

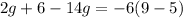
You need to solve for "g" in order to find its value. To do it, you can follow the following steps:

1. Solve the subtraction inside the parentheses

`2g+6-14g=-6(4)`

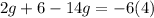
2. Solve the multiplication on the right side:

`2g+6-14g=-24`

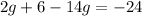
3. Apply the Subtraction property of equality by subtracting 6 from both sides of the equation:

`\begin{gathered} 2g+6-14g-(6)=-24-6 \\ 2g-14g=-30 \end{gathered}`

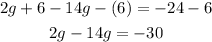
4. Add the like terms:

`-12g=-30`

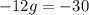
5. Finally, you can apply the Division property of equality by dividing both sides of the equation by -12:

`\begin{gathered} (-12g)/(-12)=(-30)/(-12) \\ \\ g=(5)/(2) \\ \\ g=2.5 \end{gathered}`

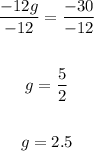
If you subsitute this value into the equation, you get:

`\begin{gathered} 2(2.5)+6-14(2.5)=-6\mleft(9-5\mright) \\ -24=-24(\text{true)} \end{gathered}`

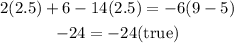
The answer is:

`g=2.5`