Answer:
4713.23 ft
Explanation:
A sketch of the problem is given below:
• The survey team was initially at point A above, the angle of elevation is 26 degrees.
,
• They moved 1500 feet closer to point B and the angle of elevation is 30 degrees.
We want to find the height, h of the mountain.
Recall from trigonometry:
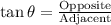
In right triangle EFB:

Likewise, in right triangle EFA:
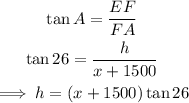
Equate the heights from the two obtained above:
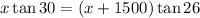
Then, solve the equation for x.
![\begin{gathered} x\tan 30\degree=(x+1500)\tan 26\degree \\ \text{Open the bracket on the right-hand side} \\ x\tan 30\degree=x\tan 26\degree+1500\tan 26\degree \\ \text{Subtract }x\tan 26\degree\text{ from both sides.} \\ x\tan 30\degree-x\tan 26\degree=x\tan 26\degree-x\tan 26\degree+1500\tan 26\degree \\ x\tan 30\degree-x\tan 26\degree=1500\tan 26\degree \\ \text{Factor out x} \\ x(\tan 30\degree-\tan 26\degree)=1500\tan 26\degree \\ \text{Divide both sides by }(\tan 30\degree-\tan 26\degree) \\ (x(\tan30\degree-\tan26\degree))/((\tan30\degree-\tan26\degree))=(1500\tan26\degree)/((\tan30\degree-\tan26\degree)) \\ \\ x=8163.5552ft \end{gathered}]()
Finally, substitute x=8163.56 ft to solve for h, the height.
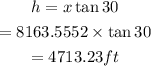
The height of the mountain is 4713.23 ft correct to 2 decimal places.