Lets write the equation in slope-intercept form
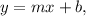
where m is the slope and b is the y-intercept.
Then, we have
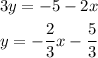
By comparing equations, we can note that the y-intercept is
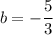
Now, the x-intercept occurs at y=0. By substituting this value into our line equation, we get
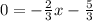
then, the x-intercept is given by

Therefore, the answer is
- x intercept is -5/2
- y-intercept is -5/3