Question

How to find the standard form and center of the circle.

Answer 1

TGiven:

`x^2+y^2+8x+22y+37=0`

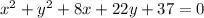
To determine the equation in standard form, we first rewrite x^2+y^2+8x+22y+37=0 into:

`\begin{gathered} x^2+y^2+8x+22y+37=0 \\ x^2+y^2+8x+22y=-37 \\ (x^2+8x)+(y^2+22y)=-37 \\ Convert\text{ x and y into square form} \\ (x^2+8x+16)+(y^2+22y+121)=-37+16+121 \\ Simplify \\ (x+4)^2+(y+11)^2=100 \end{gathered}`

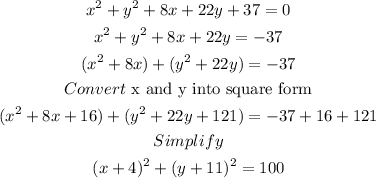
We also note the circle equation rule as shown below:

For (x-a)^2+(y-b)^2=r^2, the center is at (a,b).

Therefore, the standard form is:

`(x+4)^(2)+(y+11)^(2)=100`

And, the center is at the point (-4,-11).