Question

What is the perimeter of a rectangle with coordinates A (1, 7), B (8, 7), C (8, -3), and D (1, -3)?A35 unitsB68 unitsC70 unitsD34 units

Answer 1

Given:

There are given that the coordinates of the rectangle are:

`\begin{gathered} A:(1,7) \\ B:(8,7) \\ C:(8,-3) \\ D:(1,-3) \end{gathered}`

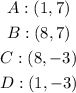
Step-by-step explanation:

To find the value of the perimeter of the rectangle, first, we need to find the distance between all sides by using the distance formula:

So,

First find the distance for side AB:

`\begin{gathered} AB=√((x_2-x_1)^2+(y_2-y_1)^2) \\ AB=√((8-1)^2+(7-7)^2) \\ AB=√((7)^2+0) \\ AB=7 \end{gathered}`

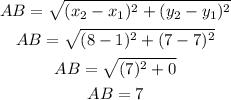
Then,

For side BC:

`\begin{gathered} BC=√((x_2-x_1)^2+(y_2-y_1)^2) \\ BC=√((8-8)^2+(-3-7)^2) \\ BC=√(100) \\ BC=10 \end{gathered}`

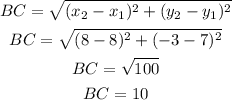
Then,

For the side CD:

`\begin{gathered} CD=√((x_2-x_1)^2+(y_2-y_1)^2) \\ CD=√((1-8)^2+(-3+3)^2) \\ CD=√((-7)^2+0) \\ CD=7 \end{gathered}`

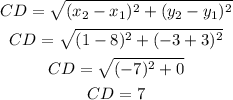
And,

For the side DA:

`\begin{gathered} DA=√((x_2-x_1)^2+(y_2-y_1)^2) \\ DA=√((1-1)^2+(-3-7)^2) \\ DA=√((100)) \\ DA=10 \end{gathered}`

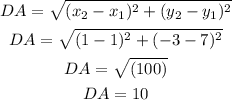
Then,

From the formula of perimeter of rectangle;

`P=AB+BC+CD+DA`

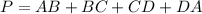
Then,

`\begin{gathered} \begin{equation*} P=AB+BC+CD+DA \end{equation*} \\ P=7+10+7+10 \\ P=14+20 \\ P=34units \end{gathered}`

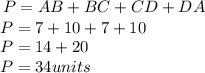
Final answer:

Hence, the correct option is D.