Question

Question has been attached below; thank you for the help!

Answer 1

Step-by-step explanation:

The question states fine the equation of the normal line of the function

`f(x)=√(x+2),at\text{ }x=-1`
`f(-1)=y_0=√(-1+2)=√(1)=1`

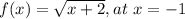
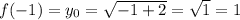
The slope os the the normal line at x= x0 is the negative reciprocal of the derivative of the function, evaluated at x=x0

`M(x_0)=-(1)/(f^(\prime)(x_0))`

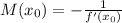
Find the derivative of f(x)

`\begin{gathered} f(x)=√(x+2) \\ f^(\prime)(x)=(x+2)^{(1)/(2)} \\ f^(\prime)(x)=(1)/(2√(x+2)) \end{gathered}`

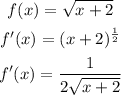
Hence,

`\begin{gathered} M(x_(0))=-(1)/(f^(\prime)(x_(0))) \\ M(x_0)=-2√(x_0+2) \end{gathered}`

Next, find the slope at the given point.

`\begin{gathered} m=M\left(−1\right)=−2 \\ M(x_0)=-2√(x_0+2) \\ M(-1)=-2√(-1+2) \\ M(-1)=-2√(1) \\ M(-1)=-2 \end{gathered}`

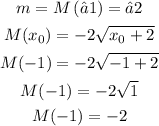
Finally, the equation of the normal line is

`\begin{gathered} y-y_0=m(x-x_0) \\ y-(1)=-2(x-(-1) \\ y-1=-2(x+1) \\ y-1=-2x-2 \\ y=-2x-2+1 \\ y=-2x-1 \end{gathered}`

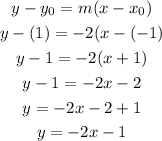
Hence,

The final answer is

`y=-2x-1`

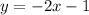
OPTION A is the correct answer