Question

If n is an integer and 2n is a factor of 1x2x3x4x5x6x7x8x9 what is the greatest possible value of n

Answer 1

Given that "n" is an integer and:

`2^n`

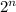
is a factor of:

`1\cdot2\cdot3\cdot4\cdot5\cdot6\cdot7\cdot8\cdot9`

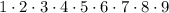
You can multiply the numbers in order to find their Product:

`1\cdot2\cdot3\cdot4\cdot5\cdot6\cdot7\cdot8\cdot9=362880`

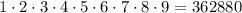
In order to find the greatest possible value of "n", you can decompose the Product found above into its Prime Factors:

`362880=2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot3\cdot3\cdot3\cdot3\cdot5\cdot7`

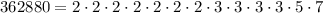
According to the Product of Powers Property, when you multiply powers that have the same base, you can add their exponents. Therefore, you can rewrite the Prime Factors in this form:

`=2^7\cdot3^4\cdot5\cdot7`

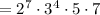
You can identify that:

`n=7`

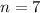
Hence, the answer is: Option B.