Question

Find the common difference of the arithmetic sequence 25, 31, 37, 43, ...OA.-5B. -6OC. 6OD. 8Reset Selection

Answer 1

Given the sequence:

`25,\text{ 31, 37, 43, . . .}`

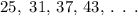
Provided that the sequence is arithmetic, to evaluate the common difference, we subtract a preceding term from its succeeding term.

This implies that

`\begin{gathered} d=a_2-a_1\text{ or a}_3-a_2 \\ where \\ d\Rightarrow common\text{ difference} \\ a_2\Rightarrow second\text{ term} \\ a_1\Rightarrow first\text{ term} \end{gathered}`

In this case,

`\begin{gathered} a_1=25 \\ a_2=31 \\ \end{gathered}`

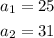
Thus, we have

`\begin{gathered} d=a_2-a_1 \\ =31-26 \\ \Rightarrow d=6 \end{gathered}`

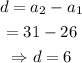
The common difference is thus 6

The correct option is