Question

Please help me ASAP!!!!

Answer 1

By moving -4 to the right hand side, we get

`\begin{gathered} |12-3x|=11+4 \\ |12-3x|=15 \end{gathered}`

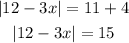
Now, by the properties of the absolute values, this last equation becomes in 2 conditions:

`\begin{gathered} a)\text{ 12-3x=15} \\ b)12-3x=-15 \end{gathered}`

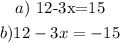
From condition a), by moving 12 to the right hand side, we get

`\begin{gathered} -3x=15-12 \\ -3x=3 \end{gathered}`

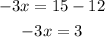
and x is given by

`\begin{gathered} x=(3)/(-3) \\ x=-1 \end{gathered}`

Now, from condition b), by moving 12 to the right hand side, we have

`\begin{gathered} -3x=-15-12 \\ -3x=-27 \end{gathered}`

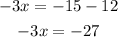
then, x is given by

`\begin{gathered} x=(-27)/(-3) \\ x=9 \end{gathered}`

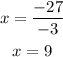
Therefore, the answer is the union of both solution, that is, the answer is the third option: x=-1, 9