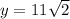Step-by-step explanation
Given the triangle
Since two of the angles are 45 and 45, this makes the third angle as 90 degrees, implying the triangle is a right-angle triangle.
We can then find the value of the missing sides below.
Using the angle 45 degrees on the left of the triangle, we will have that;
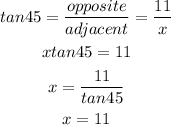
Answer: x =11
Also
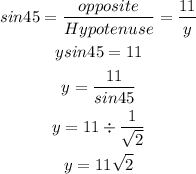
Answer: