SOLUTION:
Case: Area of triangle (maximum value) application
Given: expressions for the base and height of the triangle
length of base = x
height = 2 (24-2x)
Required: Equate Area, A(x) = (1/2) bh. Find the maximum area
Method:
The Area, A(x) is given as:

The maximum area therefore is A(x)=
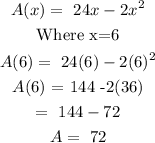
Final answer:
The maximum potential area is 72 square inches.Option (D)