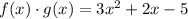Question

If f(x) = 3x+5 and g(x) = (x-1) determine an equation for f(x) x g(x)

Answer 1

The expressions for f(x) and g(x) are:

`\begin{gathered} f\mleft(x\mright)=3x+5 \\ g\mleft(x\mright)=x-1 \end{gathered}`

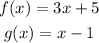
And we need to determine the following expression:

`f(x)\cdot g(x)`

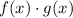
Step 1. To find f(x)*g(x) we will need to multiply the two functions:

`f(x)\cdot g(x)=(3x+5)(x-1)`

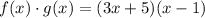
Step 2. To simplify the multiplication, we will use the distributive property:

`(a+b)(c+d)=a\cdot c+a\cdot d+b\cdot c+b\cdot d`

Which is to multiply each element of the first parentheses by the two elements in the other parentheses.

Applying the distributive property to our expression:

`f(x)\cdot g(x)=3x\cdot x+3x\cdot(-1)+5\cdot x+5\cdot(-1)`

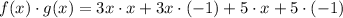
Step 3. The last step will be to simplify the operations by making the multiplications:

`f(x)\cdot g(x)=3x^2-3x+5x-5`

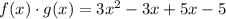
We can further simplify by combining the terms -3x and +5x into a single term which will be 2x:

`f(x)\cdot g(x)=3x^2+2x-5`

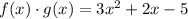
This the equation for f(x)*g(x).

Answer:

`f(x)\cdot g(x)=3x^2+2x-5`