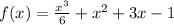Question

Given f^ prime prime (x)=x+2 and f^ prime (0)=3 and f(0) = - 1. Find f(x).

Answer 1

Given

The derivative function is given as

`f^(\prime)^(\prime)(x)=x+2`

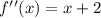
and f(0) = - 1 and f'(0) = 3

Step-by-step explanation

To determine the function,

`\begin{gathered} \int d^2y=\int(x+2)dx^2 \\ (dy)/(dx)=(x)/(2)^2+2x+C \\ f^(\prime)(0)=(0)/(2)^2+2(0)+C \\ 3=C \end{gathered}`

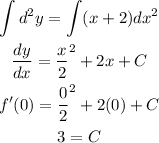
It is also given that f(0) = - 1.

`f^(\prime)(x)=(x^2)/(2)+2x+3`

Take the integral and find the function

`\begin{gathered} \int dy=\int(x^2)/(2)+2x+3dx \\ y=(x^3)/(6)+(2x^2)/(2)+3x+C \\ y=(x^3)/(6)+x^2+3x+C \\ f(x)=(x^3)/(6)+x^2+3x+C \\ -1=0+C \\ C=-1 \end{gathered}`

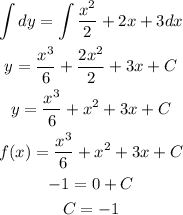
Then the function is determined as

`y=(x^3)/(6)+x^2+3x-1`

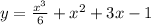
Answer

Hence the function is determined as

`f(x)=(x^3)/(6)+x^2+3x-1`