Question

10) Five cards are dealt from a standard deck of 52 cards. How many hands are possible that contain three 3's and two Kings (a full house)?

Answer 1

24

Explanation:

In a standard deck, there are 4 suits. Therefore, there are:

• 4 cards numbered 3

,

• 4 Kings.

The number of ways we can select 3 out of the 4 cards labeled 3 is:

`^4C_3`

The number of ways we can select 2 Kings out of the 4 Kings is:

`^4C_2`

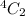
Therefore, the number of possible hands are:

`\begin{gathered} \begin{aligned} & ^4C_3*^4C_2=(4 !)/((3 !)(1 !))(4 !)/((2 !)(2 !))=(4 *3 !)/((3 !)(1 !))(4 *3 *2 !)/((2 !)(2 !)) \\ & =4*(4*3)/(2)\end{aligned} \\ =24 \end{gathered}`

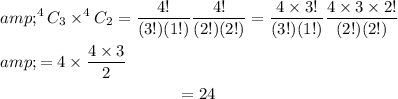
There are 24 possible hands.