To answer this question, we need to remember that:
1. If a function has been reflected in the x-axis, we have:
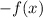
2. If a function has been translated by h units to the right, we have:
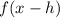
Therefore, if we have these two transformations on the function:
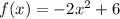
Then, if we apply the two transformations above, we have:
1. Reflection over the x-axis:
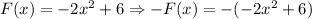
Therefore
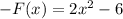
2. If we translate the function h units to the right, then we have:
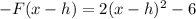
If we observe the options, we have that if we translate the function 5 units to the right, we have:
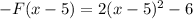
In summary, therefore, we have that the function which describes the resulting transformation is:
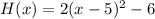
[Option C.]
We can see this in the following graph: the red parabola is the original function. The green parabola is the result of the transformation: