Given:
The function is,
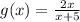
Horizontal asymtotes: it helps to describe the behavior of a graph as the input of function gets very large or very small.
The horizontal asymtotes for the given function is,
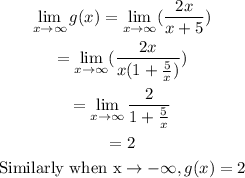
So, the equation for the horizontal asymtotes is y = 2.
Answer: Option A) y = 2.