Question

Y = 13 1 1 X - 12 12 1 1 - x - 3 6 y = 20 which ordered pair (x,y) satisfies the equations above?

Answer 1

Consider the system of equations as,

`\begin{gathered} (1)/(12)x-(1)/(12)y=13 \\ (1)/(3)x-(1)/(6)y=20 \end{gathered}`

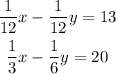
Multiply the equation 1 by 12 and the equation 2 by 6,

`\begin{gathered} x-y=156 \\ 2x-y=120 \end{gathered}`

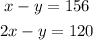
Solve the system of equations using Elimination Method.

Subtract both the equations,

`\begin{gathered} (x-y)-(2x-y)=156-120 \\ x-y-2x+y=36 \\ -x=36 \\ x=-36 \end{gathered}`

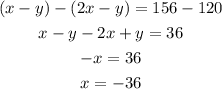
Substitute this value in equation 1,

`\begin{gathered} -36-y=156 \\ -y=156+36 \\ -y=192 \\ y=-192 \end{gathered}`

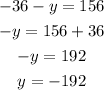
Thus, the solution of the given system of equations is (x,y) = (- 36, - 192).

Therefore, option (b) is the correct choice.