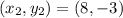Question

Find the other endpoint of the line segment with the given endpoint and midpoint Endpoint: (2,5), midpoint: (5,1)

Answer 1

We are given one endpoint (2, 5) and a midpoint (5, 1)

We are asked to find the coordinates of the other endpoint

Recall that the midpoint formula is given by

`\mleft(x_m,y_m\mright)=(x_1+x_2)/(2),(y_1+y_2)/(2)`

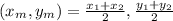
Where

`(x_m,y_m)=(5,1)_{}\text{ and }(x_1,y_1)=(2,5)`

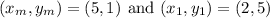
So, the other endpoint can be found as

`x_m=(x_1+x_2)/(2),y_m=(y_1+y_2)/(2)`

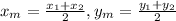
Substitute the known values

`\begin{gathered} 5=\frac{2_{}+x_2}{2},\text{ }1_{}=\frac{5_{}+y_2}{2} \\ 2*5=2_{}+x_2,\text{ }2*1_{}=5_{}+y_2 \\ 10=2_{}+x_2,\text{ }2_{}=5_{}+y_2 \\ x_2=10-2,\text{ }y_2=2-5 \\ x_2=8,\text{ }y_2=-3 \end{gathered}`

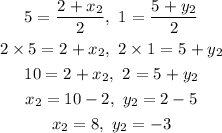
Therefore, the coordinates of the other endpoint are

`(x_2,y_2)=(8,-3)`