Given:
• m∠1 = 78 degrees
,
• m∠2 = 31 degrees.
Let's solve for the following:
• Measure of arc CE:
To find the measure of arcCE, apply the angle-arc relationship:
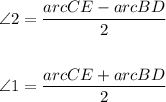
We now have the two equations.
Thus, we have:
Let x represent arcCE
Let y represent arc BD.
Thus, we have:
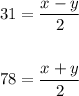
Let's solve the system of equations simultaneously.
Rewrite the first equation for x:
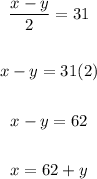
Substitute in (62+y) for x in the second equation:

Now, plug in 47 for y in either of the equations:
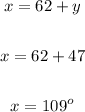
• Since x represents the measure of arcCE,:
Measure of arcCE = 109°
• Since y represents the measure of arcBD:
Measure of arcBD = 47°
ANSWER:
• Measure of arcCE = 109°
,
• Measure of arcBD = 47°