Question

Two systems of equations are given below. For each system, choose the best description of its solution. If applicable, give the solution. System Ax - 3y = −9-x + 3y = −9

Answer 1

Given: The system of equations below

`\begin{gathered} x-3y=-9 \\ -x+3y=-9 \end{gathered}`

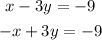
To Determine: The best description of its solution

Solution

Let us conbine the two equations

`\begin{gathered} equation1:x-3y=-9 \\ equation2:-x+3y=-9 \\ equation1+equation2 \end{gathered}`
`\begin{gathered} x+-x-3y++3y=-9+-9 \\ x-x-3y+3y=-9-9 \\ 0-0=-18 \\ 0=-18 \end{gathered}`

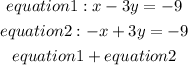
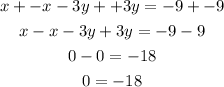
Since 0 =-18, let us plot the graph as shown below

From the above graph and calculations, we can conclude that the description of the solution is

There is no solution