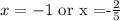Question

Problem 1:Solve using the Quadratic Formula method: 5x^2 + 7x + 2 = 0Problem 2:Solve: x2 + 2x + 7 = 0

Answer 1

The Solution to problem 1:

Given the quadratic equation below:

`5x^2+7x+2=0`

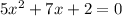
We are required to solve using the Formula method.

Step 1:

The quadratic formula is given as below:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

in this case,

`\begin{gathered} a=5 \\ b=7 \\ c=2 \end{gathered}`

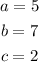
Step 2:

Substituting these values in the formula above, we get

`x=\frac{-(7)\pm\sqrt[]{7^2-4(5)(2)}}{2(5)}`
`x=\frac{-7\pm\sqrt[]{49^{}-40}}{10}=\frac{-7\pm\text{ }\sqrt[]{9}}{10}=(-7\pm3)/(10)`
`\begin{gathered} x=(-7-3)/(10)\text{ or x= }(-7+3)/(10) \\ \\ x=-(10)/(10)\text{ or x=}(-4)/(10) \\ \\ c=-1\text{ or x=}(-2)/(5) \end{gathered}`

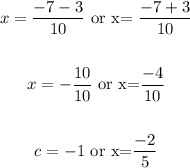
Therefore, the solution problem 1 is:

`x=-1\text{ or x =-}(2)/(5)`