In order to use this, we can use the following equation:
d = s×t
Where d is the distance, s is the speed and t is the time.
By the time Allison arrived, Austin still had 132 miles to go, then by adding the distance he has already driven to 132, we get the initial distance from home, like this:
Initial distance = distance driven + 132
Then, by subtracting 132 from both sides we can get the distance driven like this:
Initial distance - 132 = distance driven
distance driven = initial distance - 132
By calling d to the initial distance we can write:
driven distance = d - 132
Then, by replacing d - 132 for d and 40 for s into the above equation, we get an equation for the distance driven by Austin like this:
d - 132 = 40t
Similarly, for Allison:
d = 62t
By dividing the first equation by the second one, we get:
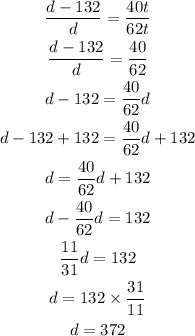
Then, Allison drove 372 miles