Question

11
The 7th term of Ap is 27 and the 12th term is 47.what is the sequence

Answer 1

3, 7, 11, 15, 19, 23, 27,.......

Explanation:

Let the first term and the common difference of the AP be a and d respectively.

`a_7 = 27 .....(given)`

Therefore,

a + (7- 1) d = 27

a + 6d = 27

a = 27 - 6d...... (1)

`a _(12) = 47.....(given)`

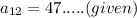
Therefore,

a + (12 - 1) d = 47

a + 11d = 47......(2)

From equations (1) & (2)

27 - 6d + 11d = 47

24 + 5d = 47

5d = 47 - 27

5d = 20

d = 20/5

d = 4

Plug d = 4 in equation (1) we find:

a = 27 - 6*4

a = 27 - 24

a = 3

Therefore,

`a_1 = a = 3`

`a_2 = a_1 + d= 3 + 4 = 7`

`a_3 = a_2 + d= 7 + 4 = 11`

`a_4 = a_3 + d= 11 + 4 = 15`

`a_5 = a_4 + d= 15 + 4 = 19`

`a_6 = a_5 + d= 19 + 4 = 23`

`a_7 = a_6 + d= 23 + 4 = 27`

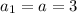
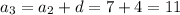
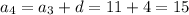
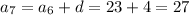
Thus, the sequence is: 3, 7, 11, 15, 19, 23, 27,.......