Question

A 0.38 m tall object is placed 0.24 m from a converging lens with a 0.19 m focal length. How tall is the image? (Remember that negative height just means the image is inverted)

Answer 1

In order to find the image's height, first let's find the image's position, using the formula below:

`(1)/(f)=(1)/(d_o)+(1)/(d_i)`

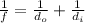
Where f is the focal length, do is the object's distance and di is the image's distance.

So, using f = 0.19 and do = 0.24, we have:

`\begin{gathered} (1)/(0.19)=(1)/(0.24)+(1)/(d_i)\\ \\ (1)/(d_i)=(1)/(0.19)-(1)/(0.24)\\ \\ (1)/(d_i)=5.263-4.167\\ \\ (1)/(d_i)=1.096\\ \\ d_i=(1)/(1.096)\\ \\ d_i=0.9124 \end{gathered}`

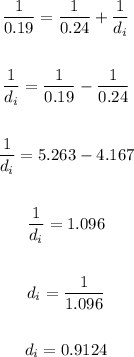
Now, to calculate the image's height, we can use the formula below:

`\begin{gathered} (h_i)/(h_o)=(-d_i)/(d_o)\\ \\ (h_i)/(0.38)=(-0.9124)/(0.24)\\ \\ h_i=(-0.9124\cdot0.38)/(0.24)\\ \\ h_i=-1.445\text{ m} \end{gathered}`

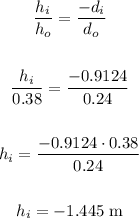
Therefore the image's height is 1.445 m.