The triangle shown has vertices:
(-4, 4)
(-9, 6)
(-8, 9)
We need to reflect these 3 points [vertices of the triangle] about the line y = x + 2.
If the reflected point(s) are of the form (u, v), then we can use the formula shown below to find the points:
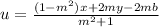
and
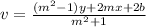
Where
x and y are the coordinates of the points we are reflecting and m is the slope fo the line and b is the y-intercept of the line about which we are making the reflection
y = x + 2
y = mx + b [slope intercept form of line]
Hence,
m = 1
b = 2
Now,
reflecting (-4,4):
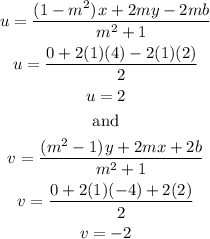
reflecting (-9,6):
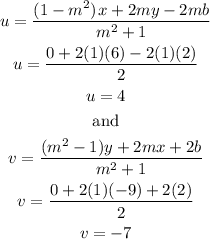
reflecting (-8,9):
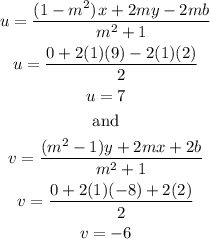
Thus, the points and their reflections are:
(-4, 4) >>> (2, -2)(-9, 6) >>> (4, -7)(-8, 9) >>> (7, -6)
Graph these points are connect as a triangle.
Shown below: