Question

An object is dropped from a height of 1600 feet off the ground. The height h of the object after t seconds can be found using the equation h=1600−16t^2. When will the object reach the ground?

(Solve by factoring & Show work.)

Answer 1

The object reaches the ground after 10 seconds.

Explanation:

The height h (in feet) of the object after t seconds is modeled by the equation:

`h=1600-16t^2`

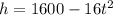
And we want to determine the time at which the object reaches the ground.

If it reaches the ground, its height h above ground will be 0. So:

`0=1600-16t^2`

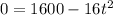
We can solve for t. First, simplify by dividing both sides by 16:

`0=100-t^2`

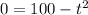
Factor using the difference of two squares pattern:

`0=(10-t)(10+t)`

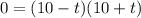
Zero Product Property:

`10-t=0\text{ or } 10+t=0`

Solve for each case:

`t=10\text{ or } t=-10`

Time cannot be negative. Thus, our only solution is:

`t=10\text{ seconds}`

The object reaches the ground after 10 seconds.