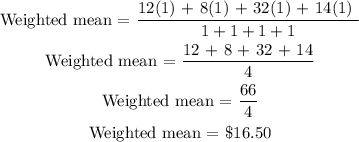Question

The value in dollars of recycling varies with the type of material. What is the weighted mean of this mixture of recyclables if compost is now worth twice as much?Paper $12/tonPlastic $8/tonCompost $16/tonAluminum $14/ton

Answer 1

Answer:

$16.50

Explanations:

The formula for calculating the wighted mean is give by:

`\begin{gathered} \text{Weighted mean = }(\sum fx)/(\sum f) \\ \text{Where x = data values} \\ f\text{ = frequency of occurence} \end{gathered}`

You can see from the table that the price of just 1 ton of each type of materials is listed.

Therefore, f = 1 for each of the materials

It is also mentioned that compost is worth twice as much as what what we have in the table, this means that the value of x for compost is $32/ton (I.e. 2 x 16)

Substituting these values into the formula:

`\begin{gathered} \text{Weighted mean = }\frac{12(1)\text{ + 8(1) + 32(1) + 14(1) }}{1+1+1+1} \\ \text{Weighted mean = }\frac{12\text{ + 8 + 32 + 14}}{4} \\ \text{Weighted mean = }(66)/(4) \\ \text{Weighted mean = \$16.50} \end{gathered}`