Question

9. A periodic deposit is made into an annuity with the given terms. Find how much the annuity will hold at the end of the specified amount of time. Round your answer to the nearest dollar. Regular deposit: $1100 Interest rate: 3.7% Frequency daily Time: 23 years Future value: $

Answer 1

Financial Maths

A sequence of equal payments (or deposits) at equal periods of time is called an annuity.

The future value of an annuity can be calculated with the formula:

`FV=A\cdot((1+i)^(n\cdot t)-1)/(i)`

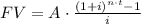
Where:

FV is the future value of the annuity

A is the periodic deposits

n is the number of compounding periods per year

i is the interest rate adjusted to the compounding periods. i = r/n where r is the APR.

t is the duration of the investment in years

The financial variables for this investment are:

A = $1100

r = 3.7% = 0.037

n = 360. Daily compounding

i = 0.037/360 = 0.000102777

It's crucial to keep as many decimals as possible in the calculations.

Applying the formula:

`FV=1100\cdot((1+0.000102777)^(360\cdot23)-1)/(0.000102777)`

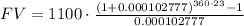
Calculating:

`FV=1100\cdot((1.000102777)^(8280)-1)/(0.000102777)`
`FV=1100\cdot13056.18`

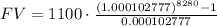
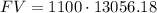
FV = $14,361,798.98

Calculation steps (in strict order)

* Add 1 + 0.00010277 = 1.00010277

* Multiply 360*23 = 8280

* Raise 1.00010277^8280 = 2.341885

* Subtract 1 = 1.341885

* Divide by 0.00010277 = 1.341885/0.00010277=13056.18

* Multiply by 1100: $14,361,798.98

Rounded to the nearest cent