Question

Brawdy Plastics, Inc., produces plastic seat belt retainers for General Motors at the Brawdy Plastics plant in Buffalo, New York. After final assembly and painting, the parts are placed on a conveyor belt that moves the parts past a final inspection station. How fast the parts move past the final inspection station depends upon the line speed of the conveyor belt (feet per minute). Although faster line speeds are desirable, management is concerned that increasing the line speed too much may not provide enough time for inspectors to identify which parts are actually defective. To test this theory, Brawdy Plastics conducted an experiment in which the same batch of parts, with a known number of defective parts, was inspected using a variety of line speeds. The following data were collected.

If required, enter negative values as negative numbers.
a. Select a scatter diagram with the line speed as the independent variable.
b. What does the scatter diagram developed in part (a) indicate about the relationship between the two variables?
c. Use the least squares method to develop the estimated regression equation (to 1 decimal). = + x d. Predict the number of defective parts found for a line speed of 25 feet per minute.
Line Speed Number of Defective Parts Found
20 23
20 21
30 19
30 16
40 15
40 17
50 14
50 11

Answer 1

All parts are solved in the attached picture

Answer 2

a. The scatter diagram created with he given data is attached

b. The scatter diagram indicates that the Number of Defective Parts found increases with Line Speed

c. The regression model is Y = 27.5 - 0.3·X

When the line speed is 25 feet per minute, the number of expected defective parts is 20 defective parts

Explanation:

The give data is presented as follows'

Line Speed;
`{}` 20, 20, 30, 30, 40, 40, 50, 50

Number of Defective;
`{}` 23, 21, 19, 16, 15, 17, 14, 11

Parts Found

a. Please find attached the scatter diagram created with Microsoft Excel

b. From the scatter diagram there is an apparent correlation between increase line speed and the number of defective parts found

c. The equation for linear regression by the least squares method is presented as follows;

Y = a + b·X

Where;

`b = (N\sum XY - \left (\sum X \right )\left (\sum Y \right ))/(N\sum X^(2) - \left (\sum X \right )^(2))`

`a = (\sum Y - b\sum X)/(N)`

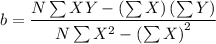
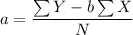
From Microsoft Excel, we have;

∑X = 280, ∑Y = 136, ∑X² = 10,800, ∑XY = 4,460, (∑X)² = 78,400, N = 8

Plugging in the values, we get;

b = (8×4,460 - 280×136)/(8×10,800 - 78,400) = -0.3

a = (136 - (-0.3)×280)/8 = 27.5

Therefore, we have the linear regression as follows;

Y = 27.5 - 0.3·X

Therefore, when the line speed is 25 feet per minute, we have;

Y = 27.5 - 0.3 × 25 = 20

The number of defective parts expected to be found when the line speed is 25 feet per minute, Y = 20 defective parts.