Question

6. Given WY with W(3, 7) and Y(13, -8), if Xpartitions WY such that the ratio of WX to XYis 3:2, find the coordinates of X.

Answer 1

(9, -2)

Step-by-step explanation:

If a point X partition a segment that starts in point (x1, y1) and ends at point (x2, y2) in a ration a:b, the coordinates of X will be equal to:

`((a)/(a+b)(x_2-x_1)+x_1,(a)/(a+b)(y_2-y_1)+y_1)`

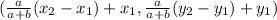
So, replacing (x1, y1) by point W(3, 7) and (x2, y2) by point Y(13, -8) and the ratio a : b by 3 : 2, we get that the coordinates of X are:

`\begin{gathered} ((3)/(3+2)(13-3)+3,(3)/(3+2)(-8-7)) \\ ((3)/(5)(10)+3,(3)/(5)(-15)+7) \\ (6+3,-9+7) \\ (9,-2) \end{gathered}`

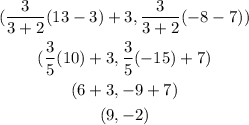
Therefore, the coordinates of X are (9, -2)